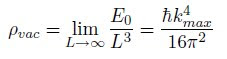What is the phenomenology of the dark sector? That is
the my question. The dark sector refers to dark energy and dark matter, which are two distinct phenomena which seem to have no direct connection other than in name. In this post I am going to talk about the cosmological constant, dark energy, and look at some landmark literature on the subject. I am going to show the origin of the 10
120 order of magnitude error that results from the quantum field theory prediction and cosmological observation. I am going to outline the physicists theoretical case and the astronomers observational case, and we will see how deceiving the cosmos can be.
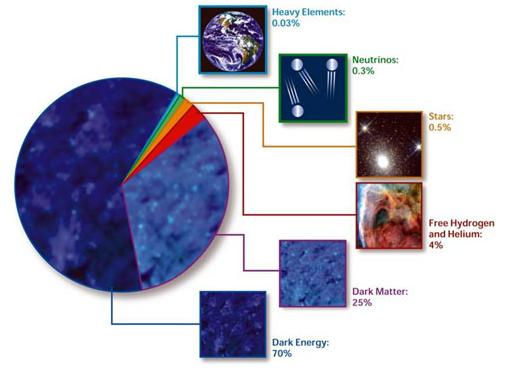
Dark energy is a form of energy attributed to the nature of empty space which increases the rate of expansion of the universe; that is if you observe a distant galaxy not only is it moving away from you in time, but the rate at which it recedes from you is accelerating. In the last 30 years or so a wide range of observations have corroborated a model of the universe wherein a majority of energy is attributed to the dark sector. The current consensus is that there is a dark energy component of our universe that represents 2/3 of the entire energy content of the universe that explains the observed cosmic acceleration. This dark energy can lead to other strange phenomena such as repulsive gravity and ultimately a universe that tears itself apart.
The composition of the cosmos.
The classic and simplest explanation for dark energy is the cosmological constant. The cosmological constant was originally introduced by Einstein as a term in his gravitational field equations in order to allow a steady state non-empty universe solution to his equations. The cosmological constant introduces a non-zero vacuum energy into the universe. This vacuum energy acts as a negative pressure (conversely a negative vacuum energy would result in a positive pressure) and this vacuum energy is known as dark energy. The idea of a vacuum containing energy is very much expected by physicists, but the observed value of the vacuum energy is what is surprising as we will see. The cosmological constant represents the particularly simple case of constant vacuum energy and is represented by the Greek character lambda (Λ). A seminal paper (also see
Weinberg 1989 or for more recent general reviews see
Carroll 2000,
Frieman et al. 2008, and
Peebels & Ratra 2002) on the topic was published in 1992 by
Carrol, Press & Turner. The abstract
The cosmological constant problem is examined in the context of both astronomy and physics. Effects of a nonzero cosmological constant are discussed with reference to expansion dynamics, the age of the universe, distance measures, comoving density of objects, growth of linear perturbations, and gravitational lens probabilities. The observational status of the cosmological constant is reviewed, with attention given to the existence of high-redshift objects, age derivation from globular clusters and cosmic nuclear data, dynamical tests of ΩΛ, quasar absorption line statistics, gravitational lensing, and astrophysics of distant objects. Finally, possible solutions to the physicist's cosmological constant problem are examined.
Roughly following Carrol et al. (1992) I will explore further the origin of the cosmological constant and the question of why the observed vacuum energy is so small in comparison to the scales of predicted by fundamental physics. We start with the Friedman equation derived from Einstein's field equations. It relates the Hubble parameter, H, to the scale factor, a, and other basic quantities.
Where the dot denotes a time derivative, G is the gravitational constant, ρ
M is the cosmological density of matter, and k is the curvature parameter which can take on values of -1,0, and +1 corresponding to a negative, flat, and hyperbolic universe geometries respectively. The Friedman equation can be viewed in terms of the contributions from matter (ρ
M), curvature (k), and vacuum energy (Λ). It is customary to parametrize these quantities in terms of their fractional value at the current epoch, that is today. We denote the current values with a subscript 0. For example the current value of Hubble's Constant is H
0~70 km/s/Mpc.
So in total then we have simplified the problem to the statement that Ω
M+Ω
k+Ω
Λ=1 for consistency with the Friedman equation. The astronomers cosmological constant problem is whether a nonzero Ω
Λ is required to achieve consistency.
The physicists cosmological constant problem begins with the statement that there are virtual vacuum states present in a vacuum due to the Heisenberg uncertainty principle. For example consider a relativistic field as the collection of harmonic oscillators of all possible frequencies, ω. The vacuum has a zero-point energy E
0 (for a scalar field φ of spinless bosons with mass m) which is the sum of contributions over all possible modes of the field, i.e. over all wave vectors
k.
We preform the sum by considering the system in a box of side length L and letting L tend to ∞. An appropriate periodic boundary condition implies λ
j=L/n
j for some integer n
j with a wave vector
kj=2π/λ
j. In the range (
kj,
kj + d
kj) there are d
kj L
j/(2 π) discrete values of
kj such that the sum becomes the integral:
The energy density of the vaccum is simply this ground state energy divided by the volume, L
3. In order to properly obtain an answer we must use ω
k2=k
2+m
2/h
2 and most importantly we impose a cutoff at a maximum wave vector k
max»m/h (note that I must use h where I mean hbar here). The result is then
The vacuum energy density can be shown to approach infinity as k
max (the physicist will recall ultraviolet catastrophe) approaches infinity therefore it is expected that there is some cutoff value near the Planck energy (E
planck is about 10
16 ergs). The logical choice is then to choose k
max=E
planck/h. The resultant prediction for this vacuum zero-point energy density is that ρ
vac ≈ 10
74 GeV
4h
-3 ≈ 10
92 g/cm
3 (the net cosmological constant is more nuanced in that it can be viewed as the sum of a number of disparate contributions including potential energies from scalar fields, zero-point fluctuations, as well as a pure cosmological constant, so only the dominant term has been addressed here), however observational cosmology has constrained ρ
obs≈ 10
-47 GeV
4h
-3 ≈ 10
-29 g/cm
3. The difference between the predicted and observed value is 120 orders of magnitude. This discrepancy is devastatingly incomprehensible large and can only be described as an
EPIC FAIL. However, it may be misleading to characterize the discrepancy this way since energy density can be expressed as a mass scale to the fourth power. Writing ρ
λ= M
vac4 we find the difference is
only 10
30. The theoretical predictions from quantum field theory have been sound in predicting vacuum effects such as the
Casimir force so there is no a priori reason to doubt predictions in this cosmological realm. The unsolved problem in physics is why doesn't the vacuum energy produce a very large cosmological constant?
Sean Carrol recently posted on the Cosmic Variance blog a list of
24 Questions for Elementary Physics for the next 100 years. Number six is,
what is the phenomenology of the dark sector? Indeed, while current observations have demonstrated the expansion of the universe is now accelerating, there are questions associated with the exact nature that are some of the most challenging problems in physics. The cosmological constant is only one form of dark energy, but what cosmologists really want to know is what is the dark energy
equation of state?
Observational support for accelerated expansion is strong from observations of type Ia supernova, standard rulers, the cosmic microwave background, gravitational lensing, etc. (the interested reader is directed to
Percival et al 2009 for results using the standard ruler baryonic acoustic oscillations technique and
Riess et al 2004 using the type Ia supernova technique), but some methods could be biased by unknown systematics. The
baryonic acoustic oscillations technique is very promising; the introduction to Percival et al 2009 explains:
Distinguishing between competing theories will only be achieved with precise measurements of the cosmic expansion history and the growth of structure within it. Among current measurement techniques for the cosmic expansion, Baryon Acoustic Oscillations (BAO) appear to have the lowest level of systematic uncertainty (Albrecht et al. 2006).
The strategies for distinguishing between a cosmological constant and other forms of dark energy all revolve around precision astrophysics measurements. Measuring the dark energy equation of state will provide a check on fundamental physics and general relativity, however it is of note that as Peebles & Ratra 2002 state:
the empirical basis [for dark energy] is not nearly as strong as it is for the standard model for particle physics: in cosmology it is not yet a matter of measuring the parameters in a well-established theory.
The gravity of the statement is that particle physics is right and observational cosmology is still just grasping in the dark. I am not a particle physicist, but to me the standard model does seem like a prediction machine and observational cosmology is just beginning to hold its own. The resolution of the dark sector may come from strange new physics like modified gravity, brane worlds, and so on (for discussions of various solutions see
Carroll et al. 2005 for cosmology of generalized modified gravity models,
Deffayet 2002 for modified brane worlds, or
Ishak et al. 2006 on measuring the cosmological equation of state). So it is possible that the accelerated expansion of the universe is an illusion of our position in the universe, a misunderstanding of fundamental physics, or an
unsatisfying tautology. No matter what it is though, everyone agrees that we need more data. That is where I come in. Consider for example, if we live in a non-homogeneous region of the universe then the solutions to Einstein's equations of general relativity would not result in the standard
Friedmann-Lamaire-Robertson-Walker metric from whence we obtained the Friedman equation. Hence our entire model would be wrong. Soon much more powerful precision astrophysics experiments (like
BOSS) will give us the observational data we need to achieve precision cosmography. I think that statements from
Célérier 2009 sum up the fundamental issue
It is commonly stated that we have entered the era of precision cosmology in which a number of important observations have reached a degree of precision, and a level of agreement with theory, that is comparable with many Earth-based physics experiments. One of the consequences is the need to examine at what point our usual, well-worn assumption of homogeneity associated to the use of perturbation theory begins to compromise the accuracy of our models. It is now a widely accepted fact that the effect of the inhomogeneities observed in the Universe cannot be ignored when one wants to construct an accurate cosmological model. Well-established physics can explain several of the observed phenomena without introducing highly speculative elements, like dark matter, dark energy, exponential expansion at densities never attained in any experiment (i.e. inflation), and the like.
In conclusion we can only say the that cosmological constant or dark energy may be an unexpected component of our universe. Currently, the best observational constraints on dark energy come from the cosmic microwave background (CMB) and type Ia supernova measurements and all the data is largely consistent. We must continue to gather data in order to quantify the large scale structure of our universe, its geometry, and its energy budget. Ultimately, in determining the energy budget of the universe, it helps to have a monetary budget here on earth. The NSF
Dark Energy Task Force has taken interest in this fundamental question so soon, we may know,
what is the phenomenology of the dark sector?

References:
Carroll, Sean M., Press, William H., & Turner, Edwin L. (1992). The cosmological constant ARA&A, 30, 499-542
Marie-Noëlle Célérier (2009). Inhomogeneities in the Universe with exact solutions of General
Relativity Invisible Universe International Conference arXiv: 0911.2597v1
Peebles, P., & Ratra, B. (2003). The cosmological constant and dark energy Reviews of Modern Physics, 75 (2), 559-606 DOI: 10.1103/RevModPhys.75.559
Will J. Percival, Beth A. Reid, Daniel J. Eisenstein, Neta A. Bahcall, Tamas Budavari, Joshua A. Frieman, Masataka Fukugita, James E. Gunn, Zeljko Ivezic, Gillian R. Knapp, Richard G. Kron, Jon Loveday, Robert H. Lupton, Timothy A. McKay, Avery Meiksin, Robert C. Nichol, Adrian C. Pope, David J. Schlegel, Donald P. Schneider, David N. Spergel, Chris Stoughton, Michael A. Strauss, Alexander S. Szalay, Max Tegmark, Michael S. Vogeley, David H. Weinberg, Donald G. York, & Idit Zehavi (2009). Baryon Acoustic Oscillations in the Sloan Digital Sky Survey Data
Release 7 Galaxy Sample MNRAS arXiv: 0907.1660v3





















 In 1066, the comet was seen in England and thought to be an omen: later that year Harold II of England died at the Battle of Hastings; it was a bad omen for Harold, but a good omen for the man who defeated him, William the Conqueror. The comet is represented on the
In 1066, the comet was seen in England and thought to be an omen: later that year Harold II of England died at the Battle of Hastings; it was a bad omen for Harold, but a good omen for the man who defeated him, William the Conqueror. The comet is represented on the